主な研究テーマ

Ｘ線極小角散乱コントラストイメージング

Ｘ線Talbot干渉計（あるいはＸ線Talbot-Lau干渉計）では、吸収像、微分位相像、ビジビリティコントラスト（小角散乱コントラスト）像という三種類の独立な画像を取得できます。図1にクロロプレン（CR）スポンジを撮影した場合の例を示します。

図1: Ｘ線Talbot-Lau干渉計により撮影されたクロロプレン（CR）スポンジの像[1]

（a）吸収像、（b）微分位相像、（c）小角散乱コントラスト像

縞走査法を例にして、これらの三枚の画像がどのように得られるかみてみましょう。縞走査法においては、回折格子（第一格子あるいは第二格子）の周期に対して、そのM分の1（Mは整数）のステップずつ回折格子を平行移動して、複数の画像を取得します。このとき第一格子の自己像と第二格子によって形成されるモアレ縞の強度は図2のように変化します。

図2: 縞走査法におけるモアレ画像の変化（M = 5の例）

ここで検出器の一つの画素（例えば図2のA）に注目すると、図3のように強度がsin関数的に変化します*1。このsin関数は、平均レベル（b）、位相（Φ）、および振幅（a）という三つの独立なパラメータによって特徴づけられます。試料がない場合（図3の黒丸）とある場合（青丸）のデータから、図1の三種類の画像が得られます。すなわち、図3のbs/b0から吸収像が、Φs-Φ0から微分位相像が、さらに(as/bs)/(a0/b0)からビジビリティコントラスト像が得られます*2。ビジビリティコントラスト像は以下で述べるように小角散乱コントラスト像とも呼ばれます。

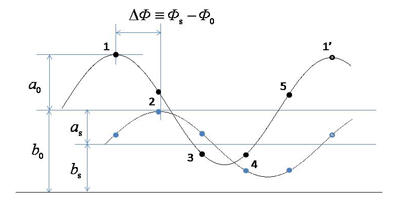
図3: 縞走査を行ったときの1画素（例えば図2の点A）における強度の変化（黒丸: 試料なし; 青丸: 試料あり; M=5の例）。試料がないときのパラメータは下付添字0で、試料がある場合は下付添字sで表してある。塗りつぶされていない丸（1’）は回折格子がちょうど1周期分移動したときの強度。

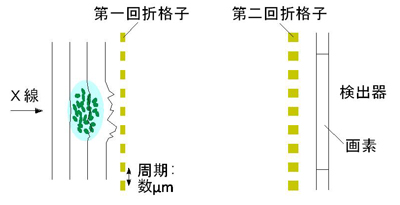
ビジビリティコントラストが生じるメカニズムについても簡単に紹介しましょう。ビジビリティコントラストは、図4のように、試料の中に回折格子の周期と同程度で、かつ検出器で解像できない大きさの微小な構造がある場合に生じることが我々の研究により明らかになっています[2]。これはちょうど可視光が磨りガラスを透過する様子に似ています。このような微小な構造（図4の場合μmサイズ）は、一般に極小角散乱と呼ばれる散乱を生じることが知られています。すなわち得られたビジビリティコントラスト画像は、小角Ｘ線散乱と関係する物理量の分布を二次元的に画像化したものであると言えます*3。これが小角散乱コントラスト像と呼ばれる理由です。このことを積極的に利用すれば、通常の（極）小角Ｘ線散乱法（SAXS）によって得られる情報（微小構造のサイズや形状など）を二次元的に画像化したり、さらにはトモグラフィの原理によって三次元的にマッピングしたりすることができます[3]。

図4: 回折格子の周期（図では数μm）と同程度の大きさで、検出器で解像できないスケールの微小な構造がＸ線の波面に空間的なフラクチュエーションを生じる様子。このフラクチュエーションがモアレ縞のビジビリティを減少させる[2]。
[1] W. Yashiro, S. Harasse, K. Kawabata, H. Kuwabara, T. Yamazaki, and A. Momose, "Distribution of unresolvable anisotropic microstructures revealed in visibility-contrast images using x-ray Talbot interferometer", Phys. Rev. B 84 (2011) 094196.
[2] W. Yashiro, Y. Terui, K. Kawabata, and A. Momose, “On the origin of visibility contrast in x-ray Talbot interferometry”, Opt. Exp. 18 (2010) 16890-16901.
[3] W. Yashiro, S. Harasse, H. Kuwabara, K. Kawabata, and A. Momose, “Quantitative visibility-contrast tomography in the X-ray Talbot interferometry”, AIP Conf. Proc. 1466 (2012) 211-216.

*1光源サイズが十分に小さくて（第一格子の位置での空間コヒーレンス長が十分大きいとみなせて）、さらに単色Ｘ線とみなせるような理想的な場合には、sin関数ではなく三角波になる。光源サイズが大きいなどの理由で高次のFourier成分が無視できる場合にはsin関数とみなせる。

*2一般にビジビリティは(Imax-Imin)/(Imax+Imin)で定義される。ここでImaxは強度の最小値、Iminは強度の最小値を表している。試料がある場合とない場合のビジビリティの比からビジビリティコントラスト像を求めることができる。

*3我々の研究により、ビジビリティコントラストは、微小な構造により乱れた波面の（回折格子のラインに垂直な方向の）自己相関関数で与えられることが示されている[2]。これはまた（極）小角Ｘ線散乱強度の散乱角依存性（回折格子のライン方向の成分は積分したもの）をFourier変換したものに相当する。